Power Grid Simulation

Introduction
The underlying solver algorithms used in power grid (PG) simulation today are derivations of circuit simulation algorithms first developed many decades ago. In fact, the 40^th anniversary of SPICE (a widely used circuit simulator), was celebrated in 2011. As such, it is understandable that many engineers have a jaundiced view towards claims of improved PG simulation performance. Nevertheless, the cumulative effects of new algorithms and upgraded computing resources over the past decade have indeed resulted in performance improvements.

Let’s take a look at how various developments in algorithms and computing resources have contributed to PG simulation improvements. First, we’ll go over the basics of PG simulation, which first formulates the equation  , then computes the solution . Next, we’ll explore the various developments that have resulted in improved efficiencies when computing .

Power Grid Simulation Basics
In my last article, I gave you an overview of power grid analysis (PGA). Let’s recap a few important points before we move on. The main take away for this section is the mechanics of how a power grid can be modeled mathematically in the matrix form  where:

• A is a matrix representing the power grid resistance, capacitance, and inductive element values.
• is a vector representing the node voltages and branch currents in the power grid.
•   is a vector representing the standard cell and macro current sources, and voltage bump values.

Once the mathematical model has been constructed, the solution is simply .

A PG analysis tool views a design as consisting of two distinct, but related, netlists (Figure 1). The design netlist contains a description of the circuit elements and the interconnections among them. The PG netlist consists of the power and ground networks associated with different voltage domains respectively. In a digital flow, the circuit elements are typically standard cells, or other hard intellectual property (IP) macros, such as register files or memory blocks.

Figure 1. PG and design networks.

One of the steps in a PGA flow is to annotate the PG netlist with the parasitic resistance, capacitance, and inductances extracted from the layout to produce a parasitic RCL netlist. PG simulation computes the currents and voltages in the parasitic PG netlist when driven by the equivalent current source waveforms of the underlying cells and macros (Figure 2).

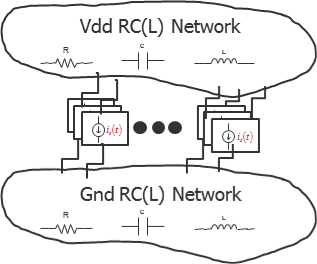
Figure 2. Parasitic PG circuit network.

In static analysis, each current source is assigned a single value representative of a typical activity, and the parasitic PG netlist only contains resistors, and no energy storage elements (no capacitors nor inductors). In dynamic analysis, current sources have time-dependent waveforms, and the PG netlist has resistors, capacitors, and inductors.

A PG simulation can be decomposed into two major steps, problem formulation and solver computation (Figure 3).  During the problem formulation, a mathematical model of the parasitic PG netlist is constructed using circuit analysis equations. In turn, the solver computes the solution to this mathematical model.

Figure 3. Power grid simulation flow.

The problem formulation step uses the current nodal equations as specified by Kirchoff’s current law (KCL), which specifies that the sum of the currents entering and leaving a given node should be zero. There will be an equation for each node in the parasitic PG netlist other than the common ground node (datum).

Figure 4 shows a 3-node parasitic PG netlist with 3 parasitic resistors and 2 current sources. Since there are two non-datum nodes, there will only be two nodal equations.

Figure 4. Nodal equations.

The matrix form of the equation is shown in Figure 5. The solver step computes the values of the node voltages v₁ and v_2, and is shown as .

Figure 5. Matrix representation and symbolic solution.

Representation of energy storage elements (such as capacitors and inductors) are shown in Figure 6.

Figure 6. Energy storage elements.

The KCL analysis treats different elements identically. In Figure 7, the same nodal analysis is performed to obtain three nodal analysis equations, with derivatives for the capacitance branch currents, and with integrals for the inductance branch voltages.

Figure 7. Nodal analysis with RLC elements.

Typically, the integration is computed numerically using a Backward Euler or Trapezoidal discretization integration scheme, where an equivalent companion model is inserted at each timestamp (Figure 8).

Figure 8. Backward Euler and Trapezoidal companion models.

These transforms convert the energy storage elements to two parallel branches—one for a conductance and the other for a current source (Figure 9). The solver step performs the same calculations, except there are multiple solver steps for each time step.

Figure 9. RLC circuit with Trapezoidal companion models.

In summary, a power grid simulator must first formulate the mathematical model of the parasitic PG netlist as , then compute the solution . The capacitors and inductors are discretized into companion models at each time step, so a solution  must be computed at each time point.

Direct Solvers
Direct solvers compute the solution  using operations similar to Gauss elimination. At the end of the algorithm, the solution  is available for reuse with different  excitation vectors, such as different sets of standard cells, or macros that are active. Direct solver algorithms do not invert the matrix A to form , but instead keep it as the product of the two matrices  L x U (if A is asymmetric) or  (if A is symmetric). The algorithm to compute L x U is called LU factorization, and the algorithm to compute   is called a Cholesky factorization.

For a dense matrix A, where most of the entries are non-zero, direct solver algorithms have complexity . However, power grids are very sparse, since the majority of the nodes in a parasitic PG netlist connect to only 2-4 neighbors at most. This means that most of the entries in the matrix A are zeros or sparse.

Sparse direct solver algorithms have a reported complexity of , as long as the sparsity is not significantly decreased during the algorithm execution. The term fill-in describes the situation when a zero entry becomes non-zero.

To understand how a fill-in can occur, it is instructive to walk through a small example. In the algorithm, the goal is to cause a specific column entry in row to become zero by adding or subtracting another row. This is the variable elimination step that you would need to do if you were solving the equations manually. Figure 10 shows a small circuit, along with the nodal equations that generate the matrix A. Figure 11 shows a subset trace of the elementary row operations for a good matrix ordering. Figure 12 show a matrix ordering where the rows associated with the variables and  have been exchanged. As you can see, a fill-in has occurred in the zero entry located at row=2, column=3.

Figure 10. Fill-in circuit example.

Figure 11. Elementary row operations.

Figure 12. Elementary row operation with fill-in.

Fill-ins are undesirable, because additional memory has to be allocated to accommodate the new values, and they increase the computational load for the direct solver algorithm. In the worst case, the algorithm complexity can approach , where n is the size of the matrix.

Over the past five years, there has been very active research activity in creating direct solver re-ordering algorithms to minimize fill-in. A re-ordering is a swapping or permutation of rows or columns in the matrix A and vectors x and b. In fact, most algorithms will perform column permutations to avoid having the smallest row entry as the pivot or diagonal entry, because division by small values can cause numerical issues.

Rather than going through the details of the various re-ordering algorithms, let’s look at screenshots of the sparsity patterns before and after the re-ordering algorithms are applied. The white regions are zero entries, while the black/red/blue regions are the non-zero entries (Figures 13-14).

Figure 13. Sparse matrix re-ordering example 1.

Figure 14. Sparse matrix re-ordering example 2.

A natural question is what runtime impact these re-ordering algorithms have when solving real circuit matrices. Fortunately, there are studies comparing different direct solver algorithms using matrices generated from circuits. Figure 15 shows runtimes for various sparse matrix solver algorithms. Sparse1.3 (used in Spice3) dates from 1988, and shows its age when compared with the more recent packages.

Figure 15. Solve runtimes for various re-ordering algorithms.

Figure 16 shows the various characteristics of the benchmark circuits.

Figure 16. Solver benchmark circuit characteristics.

As can be seen from the benchmark runtimes (Figure 17), new re-ordering schemes developed in the academic research community have yielded improvements in direct solver runtimes. A careful reading of the research literature would show that it is the accumulated benefits of various re-ordering algorithms that have yielded these improvements, rather than one single silver bullet breakthrough algorithm.

Figure 17. Graph of benchmark runtimes.

Hybrid Solvers
Iterative solvers are another class of solvers that can be used for PG simulation. Rather than compute a solution to , iterative solvers produce a sequence of solutions  in k iterations. Each successive  gets closer to the correct solution, and the iteration stops when the difference between two successive iterations is within some tolerance . Figure 18 shows examples of iterative solvers based on the decomposition of the matrix A. Gauss-Seidel uses , while Gauss-Jacob uses any .

Figure 18. Iterative solver formulas

Iterative methods have issues such as large iteration counts and non-convergence, but have smaller memory requirements than direct methods.  Various techniques such as conjugate gradient with pre-conditioners have been developed to mitigate the issues. However, the biggest distracter is that for a transient simulation of a parasitic PG netlist, each timestep requires the execution of the iterative method. In contrast, the factorized matrix A=LU or A= can be re-used at multiple timesteps.

Domain decomposition is a technique where multiple sub-problems are solved independently with iteration steps to reconcile differences at the interfaces of the sub-problems. This suggests a hybrid approach, where the sub-blocks are solved using direct methods, while using iterative steps at the top level. This technique allows the use of factorized matrices during transient simulations with the memory footprint of an iterative method.

The advantage of the hybrid approach is that it allows a distributed computing approach, where the PG solver workload is spread among multiple machines, rather than in one shared large memory machine. Initial results from the research community are promising. Figure 19 shows a domain decomposition scheme and its runtime on a computing cluster. N(M) is the number of nodes in millions, C is the components (VDD/VSS), P is the number of cores being utilized, and tp(s) is the CPU time in seconds.

Figure 19. Domain decomposition configuration and runtimes.

Scalability of the hybrid approach also looks promising, as shown in Figure 20, despite the sub-optimality introduced by the relative small memory size of 1.2 GB available to each distributed core. The resulting increase in network traffic probably impacted the runtimes negatively.

Figure 20. Domain decomposition scalability.

Figure 21 illustrates a case where a domain that is too small negatively impacts the runtimes. In this example, the same circuit is partitioned into 1, 4, 16, 64, 256, and 1024 domains. With the single partition scenario, the runtime is dominated entirely by the direct solver. In the small partition size scenario, the runtime is probably worse than that of the purely iterative method, due to the domain decomposition overhead and the lack of a pre-conditioner to reduce the iteration counts.

Figure 21. Domain decomposition runtime vs. partition size.

The hybrid solver approach, based on domain decomposition using an amalgam of direct solver and iterative methods, is a promising approach for allowing distributed computing for PG simulation. A recent ICCAD paper even used the MapReduce terminology to describe their distributed computing approach for PG simulation.  The domain decomposition algorithm appears to be scalable, and easily fits within the streaming data flow necessary for the MapReduce framework.

Summary
This article covers a great deal of material about PG simulation, ranging from problem formulation to a survey of the recent algorithm developments. You probably learned more about   and its solution  than you expected, but such a background is necessary to appreciate the impact of the various algorithm developments. This is especially relevant in regards to allowing a truly distributed computing PG solver, rather than today’s single box multi-thread solution.

In the end, I hope I convinced you that, despite the relative old age of the underlying PG solver algorithms, there is still scope for performance improvements.

References/Further Reading

L. T. Pillage, R. A. Rohrer, and C. Visweswariah. Electronic Circuit and System Simulation Methods. McGraw Hill, 1994.

Farid, Najm. Circuit Simulation. Wiley-IEEE Press, 2010.

Kron, Gabriel, “A Method to Solve Very Large Physical Systems in Easy Stages,” Circuit Theory, Transactions of the IRE Professional Group on , vol.PGCT-2, no., pp.71,90, December 1953.

Rohrer, R.A., “Circuit partitioning simplified,” Circuits and Systems, IEEE Transactions on , vol.35, no.1, pp.2,5, Jan 1988.

L. Grigori, E. Boman, S. Donfack, and T. A. Davis, Hypergraph-based unsymmetric nested dissection ordering for sparse LU factorization, SIAM Journal on Scientific Computing, Vol 32, Issue 6, 2010, pp 3426-3446.

Yanqing Chen, Timothy A. Davis, William W. Hager, Sivasankaran Rajamanickam, Algorithm 887: CHOLMOD, Supernodal Sparse Cholesky Factorization and Update/Downdate, ACM Transactions on Mathematical Software, Vol 35, Issue 3, 2008, pp 22:1 – 22:14.

Timothy A. Davis, Ekanathan Palamadai Natarajan,Algorithm 907: KLU, A Direct Sparse Solver for Circuit Simulation Problems, ACM Transactions on Mathematical Software, Vol 37, Issue 6, 2010, pp 36:1 – 36:17.

The University of Florida Sparse Matrix Collection T. A. Davis and Y. Hu, ACM Transactions on Mathematical Software, Vol 38, Issue 1, 2011, pp 1:1 – 1:25. http://www.cise.ufl.edu/research/sparse/matrices.

T. Yu, Z. Xiao, and M. D. F. Wong. Efficient parallel power grid analysis via Additive Schwarz Method. Computer-Aided Design (ICCAD), 2012 IEEE/ACM International Conference on , vol., no., pp.399,406, 5-8 Nov. 2012.

Kai Sun; Quming Zhou; Mohanram, K.; Sorensen, D.C., “Parallel domain decomposition for simulation of large-scale power grids,” Computer-Aided Design, 2007. ICCAD 2007. IEEE/ACM International Conference on , vol., no., pp.54,59, 4-8 Nov. 2007

Jia Wang; Xuanxing Xiong, “Scalable power grid transient analysis via MOR-assisted time-domain simulations,” Computer-Aided Design (ICCAD), 2013 IEEE/ACM International Conference on , vol., no., pp.548,552, 18-21 Nov. 2013

Ting Yu; Zigang Xiao; Wong, M.D.F., “Efficient parallel power grid analysis via Additive Schwarz Method,” Computer-Aided Design (ICCAD), 2012 IEEE/ACM International Conference on , vol., no., pp.399,406, 5-8 Nov. 2012